Grade 5 GT Mathematics
Expressions & Equations (6.EE/7.EE)
In this unit, students understand the use of variables in mathematical expressions. They write expressions and equations that correspond to given situations, evaluate expressions, and use expressions and formulas to solve problems. Students understand that expressions in different forms can be equivalent, and they use the properties of operations to rewrite expressions in equivalent forms. Students know that the solutions of an equation are the values of the variables that make the equation true. Students use properties of operations and the idea of maintaining the equality of both sides of an equation to solve simple one-step equations. Students construct and analyze tables, such as tables of quantities that are in equivalent ratios, and they use equations (such as 3x = y) to describe relationships between quantities.
Students use the arithmetic of rational numbers as they formulate expressions and equations in one variable and use these equations to solve problems. Students will understand and use properties of operations to generate equivalent expressions. Students use and solve real-life mathematical problems using numerical and algebraic expressions and equations. Also, students will use variables to represent quantities in a real-world or mathematical problem to construct and solve simple equations and inequalities in one and two step. In gaining the understanding of solving the one and two-step equations and inequalities, students will reason about the quantity of their solutions.
Students use the arithmetic of rational numbers as they formulate expressions and equations in one variable and use these equations to solve problems. Students will understand and use properties of operations to generate equivalent expressions. Students use and solve real-life mathematical problems using numerical and algebraic expressions and equations. Also, students will use variables to represent quantities in a real-world or mathematical problem to construct and solve simple equations and inequalities in one and two step. In gaining the understanding of solving the one and two-step equations and inequalities, students will reason about the quantity of their solutions.
NOTE - The "Background Info. and Guided Practice" links require a free registration to use the LearnZillion content. Parents can create a free "Teacher" account here. Once logged in you can access the "Background Info. & Guided Practice" videos without interruption.
What will my child learn?
Students will:
Apply and extend previous understandings of arithmetic to algebraic expressions.
6.EE.A.1
Write and evaluate numerical expressions involving whole-number exponents.
6.EE.A.2
Write, read, and evaluate expressions in which letters stand for numbers.
6.EE.A.2.A
Write expressions that record operations with numbers and with letters standing for numbers. For example, express the calculation "Subtract y from 5" as 5 - y.
6.EE.A.2.B
Identify parts of an expression using mathematical terms (sum, term, product, factor, quotient, coefficient); view one or more parts of an expression as a single entity. For example, describe the expression 2 (8 + 7) as a product of two factors; view (8 + 7) as both a single entity and a sum of two terms.
6.EE.A.2.C
Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole-number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations). For example, use the formulas V = s3 and A = 6 s2 to find the volume and surface area of a cube with sides of length s = 1/2.
6.EE.A.3
Apply the properties of operations to generate equivalent expressions. For example, apply the distributive property to the expression 3 (2 + x) to produce the equivalent expression 6 + 3x; apply the distributive property to the expression 24x + 18y to produce the equivalent expression 6 (4x + 3y); apply properties of operations to y + y + y to produce the equivalent expression 3y.
6.EE.A.4
Identify when two expressions are equivalent (i.e., when the two expressions name the same number regardless of which value is substituted into them). For example, the expressions y + y + y and 3y are equivalent because they name the same number regardless of which number y stands for.
Reason about and solve one-variable equations and inequalities.
6.EE.B.5
Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? Use substitution to determine whether a given number in a specified set makes an equation or inequality true.
6.EE.B.6
Use variables to represent numbers and write expressions when solving a real-world or mathematical problem; understand that a variable can represent an unknown number, or, depending on the purpose at hand, any number in a specified set.
6.EE.B.7
Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px = q for cases in which p, q and x are all non-negative rational numbers.
6.EE.B.8
Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams.
Represent and analyze quantitative relationships between dependent and independent variables.
6.EE.C.9
Use variables to represent two quantities in a real-world problem that change in relationship to one another; write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation. For example, in a problem involving motion at constant speed, list and graph ordered pairs of distances and times, and write the equation d = 65t to represent the relationship between distance and time.
Use properties of operations to generate equivalent expressions.
7.EE.A.1
Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
7.EE.A.2
Understand that rewriting an expression in different forms in a problem context can shed light on the problem and how the quantities in it are related. For example, a + 0.05a = 1.05a means that "increase by 5%" is the same as "multiply by 1.05."
Solve real-life and mathematical problems using numerical and algebraic expressions and equations.
7.EE.B.3
Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies. For example: If a woman making $25 an hour gets a 10% raise, she will make an additional 1/10 of her salary an hour, or $2.50, for a new salary of $27.50. If you want to place a towel bar 9 3/4 inches long in the center of a door that is 27 1/2 inches wide, you will need to place the bar about 9 inches from each edge; this estimate can be used as a check on the exact computation.
7.EE.B.4
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
7.EE.B.4.A
Solve word problems leading to equations of the form px + q = r and p(x + q) = r, where p, q, and r are specific rational numbers. Solve equations of these forms fluently. Compare an algebraic solution to an arithmetic solution, identifying the sequence of the operations used in each approach. For example, the perimeter of a rectangle is 54 cm. Its length is 6 cm. What is its width?
7.EE.B.4.B
Solve word problems leading to inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem. For example: As a salesperson, you are paid $50 per week plus $3 per sale. This week you want your pay to be at least $100. Write an inequality for the number of sales you need to make, and describe the solutions.
Students will:
Apply and extend previous understandings of arithmetic to algebraic expressions.
6.EE.A.1
Write and evaluate numerical expressions involving whole-number exponents.
- Check for Understanding: Positive and Zero Exponents | Writing Expressions with Exponents | Writing Expressions with Exponents Word Problems | Evaluating Expressions with Exponents | Evaluating Exponent Expression Word Problems
- Enrichment Tasks: Sierpinski's Carpet | Seven to the What?
6.EE.A.2
Write, read, and evaluate expressions in which letters stand for numbers.
- Check for Understanding: Evaluating Expressions with Variables Word Problems
- Enrichment Tasks: Distance to School
6.EE.A.2.A
Write expressions that record operations with numbers and with letters standing for numbers. For example, express the calculation "Subtract y from 5" as 5 - y.
- Background Info. & Guided Practice
- Check for Understanding: Writing Expressions | Writing Expressions 2 | Writing Expressions with Variables Word Problems |
- Enrichment Tasks: Writing Expressions
6.EE.A.2.B
Identify parts of an expression using mathematical terms (sum, term, product, factor, quotient, coefficient); view one or more parts of an expression as a single entity. For example, describe the expression 2 (8 + 7) as a product of two factors; view (8 + 7) as both a single entity and a sum of two terms.
- Check for Understanding: Identifying Parts of Expressions
6.EE.A.2.C
Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole-number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations). For example, use the formulas V = s3 and A = 6 s2 to find the volume and surface area of a cube with sides of length s = 1/2.
- Check for Understanding: Evaluate Expressions in One Variable | Evaluate Expressions in Two Variables | Evaluating Expression with Variables Word Problems
- Enrichment Tasks: Rectangular Perimeter 1
6.EE.A.3
Apply the properties of operations to generate equivalent expressions. For example, apply the distributive property to the expression 3 (2 + x) to produce the equivalent expression 6 + 3x; apply the distributive property to the expression 24x + 18y to produce the equivalent expression 6 (4x + 3y); apply properties of operations to y + y + y to produce the equivalent expression 3y.
- Check for Understanding: Combining Like Terms | Equivalent Forms of Expressions 1
- Enrichment Tasks: Pan Balance-
6.EE.A.4
Identify when two expressions are equivalent (i.e., when the two expressions name the same number regardless of which value is substituted into them). For example, the expressions y + y + y and 3y are equivalent because they name the same number regardless of which number y stands for.
- Background Info. & Guided Practice | More Background Info. on equations using balance scales
- Video: Commutative and Associative Equations
- Check for Understanding: Equivalent Forms of Expressions 1
- Enrichment Tasks: Equivalent Expressions | Rectangular Perimeter 2
Reason about and solve one-variable equations and inequalities.
6.EE.B.5
Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? Use substitution to determine whether a given number in a specified set makes an equation or inequality true.
- Check for Understanding: Solving Equations and Inequalities Through Substitution
- Enrichment Tasks: Log Ride
6.EE.B.6
Use variables to represent numbers and write expressions when solving a real-world or mathematical problem; understand that a variable can represent an unknown number, or, depending on the purpose at hand, any number in a specified set.
- Check for Understanding: Constructing and Solving Linear Equations Word Problems
- Enrichment Tasks: Firefighter Allocation | Triangular Tables
6.EE.B.7
Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px = q for cases in which p, q and x are all non-negative rational numbers.
- Check for Understanding: One-Step Equation Intuition | One-Step Equations | One-Step Equations With Multiplication | Constructing and Solving Linear Equations Word Problems
- Enrichment Tasks: Morning Walk | Fruit Salad
6.EE.B.8
Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams.
- Check for Understanding: Use Inequalities to Describe Real World Contexts | Inequalities on a Number Line
- Enrichment Tasks: Fishing Adventures 1
Represent and analyze quantitative relationships between dependent and independent variables.
6.EE.C.9
Use variables to represent two quantities in a real-world problem that change in relationship to one another; write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation. For example, in a problem involving motion at constant speed, list and graph ordered pairs of distances and times, and write the equation d = 65t to represent the relationship between distance and time.
- Check for Understanding: Dependent and Independent Variables
- Enrichment Tasks: Chocolate Bar Sales
Use properties of operations to generate equivalent expressions.
7.EE.A.1
Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
- Background Info. & Guided Practice
- Check for Understanding: Combining Like Terms with Distributions | Manipulating Linear Expressions with Rational Coefficients
- Enrichment Tasks: Writing Expressions* | TV Sales | Equivalent Expressions?*
7.EE.A.2
Understand that rewriting an expression in different forms in a problem context can shed light on the problem and how the quantities in it are related. For example, a + 0.05a = 1.05a means that "increase by 5%" is the same as "multiply by 1.05."
- Check for Understanding: Interpreting Linear Expressions
- Enrichment Tasks: Ticket to Ride | Miles to Kilometers*
Solve real-life and mathematical problems using numerical and algebraic expressions and equations.
7.EE.B.3
Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies. For example: If a woman making $25 an hour gets a 10% raise, she will make an additional 1/10 of her salary an hour, or $2.50, for a new salary of $27.50. If you want to place a towel bar 9 3/4 inches long in the center of a door that is 27 1/2 inches wide, you will need to place the bar about 9 inches from each edge; this estimate can be used as a check on the exact computation.
- Background Info. & Guided Practice
- Check for Understanding: Average Word Problems | Discount, Tax, and Tip Word Problems | Mark-up and Commission Word Problems | Multi-Step Rational Number Word Problems
- Enrichment Tasks: Who is the better batter? | Spicy Veggies | Stained Glass*
7.EE.B.4
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
- Check for Understanding: Linear Equation Word Problems | Two-Step Equations
- Enrichment Tasks: Bookstore Account
7.EE.B.4.A
Solve word problems leading to equations of the form px + q = r and p(x + q) = r, where p, q, and r are specific rational numbers. Solve equations of these forms fluently. Compare an algebraic solution to an arithmetic solution, identifying the sequence of the operations used in each approach. For example, the perimeter of a rectangle is 54 cm. Its length is 6 cm. What is its width?
- Check for Understanding: Linear Equation Word Problems | Two-Step Equations
- Enrichment Tasks: Guess My Number*
7.EE.B.4.B
Solve word problems leading to inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem. For example: As a salesperson, you are paid $50 per week plus $3 per sale. This week you want your pay to be at least $100. Write an inequality for the number of sales you need to make, and describe the solutions.
- Check for Understanding: One-Step Inequalities | Two-Step Inequalities | Interpreting and Solving Linear Inequalities
- Enrichment Tasks: Fishing Adventures 2* | Sports Equipment Set*
|
What are some signs of student mastery?
|
Tools & Technology
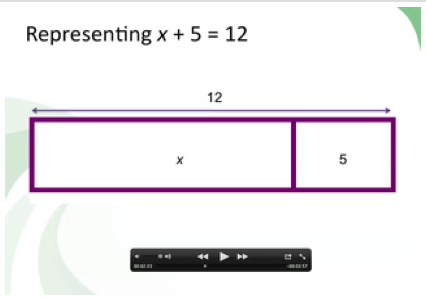
This video teaches how tape diagrams can be used to solve and understand the solutions to algebraic equations. |
More 4 U
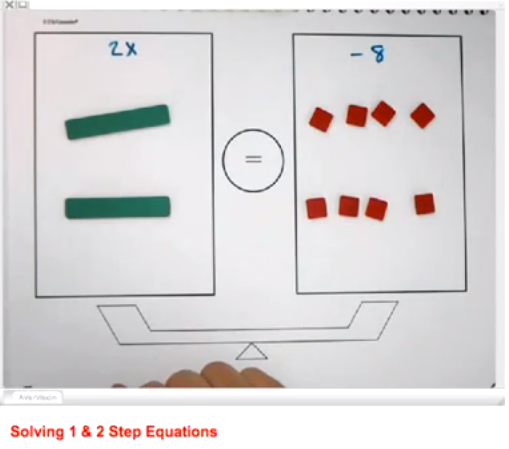
Have you ever heard your child talk about using Algebra Tiles in math class? Watch this video on "Solving One and Two Step Equations with Algebra Tiles." These videos explain how Algebra Tiles can be used to:
|