Grade 5 GT Mathematics
The Number System (6.NS/7.NS)
Throughout this unit, students use the meaning of fractions, the
meanings of multiplication and division, and the relationship between
multiplication and division to understand and explain why the
procedures for dividing fractions make sense. Students use these
operations to solve problems. Students extend their previous
understandings of number and the ordering of numbers to the full system
of rational numbers, which includes negative rational numbers, and in
particular negative integers. They reason about the order and absolute
value of rational numbers and about the location of points in all four
quadrants of the coordinate plane.
Also during this unit, students develop a unified understanding of number, recognizing fractions, decimals (that have a finite or a repeating decimal representation), and percents as different representations of rational numbers. Students extend addition, subtraction, multiplication, and division to all rational numbers, maintaining the properties of operations and the relationships between addition and subtraction, and multiplication and division. By applying these properties, and by viewing negative numbers in terms of everyday contexts (e.g., amounts owed or temperatures below zero), students explain and interpret the rules for adding, subtracting, multiplying, and dividing with negative numbers.
Also during this unit, students develop a unified understanding of number, recognizing fractions, decimals (that have a finite or a repeating decimal representation), and percents as different representations of rational numbers. Students extend addition, subtraction, multiplication, and division to all rational numbers, maintaining the properties of operations and the relationships between addition and subtraction, and multiplication and division. By applying these properties, and by viewing negative numbers in terms of everyday contexts (e.g., amounts owed or temperatures below zero), students explain and interpret the rules for adding, subtracting, multiplying, and dividing with negative numbers.
NOTE - The "Background Info. and Guided Practice" links require a free registration to use the LearnZillion content. Parents can create a free "Teacher" account here. Once logged in you can access the "Background Info. & Guided Practice" videos without interruption.
What will my child learn?
Students will:
Apply and extend previous understandings of multiplication and division to divide fractions by fractions.
6.NS.A.1
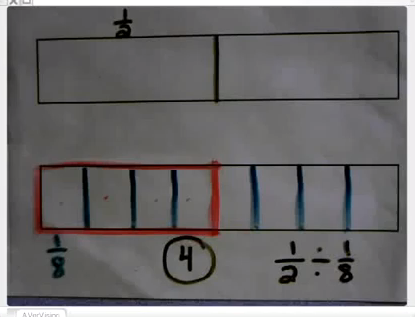
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?.
Compute fluently with multi-digit numbers and find common factors and multiples.
6.NS.B.2
Fluently divide multi-digit numbers using the standard algorithm.
6.NS.B.3
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
6.NS.B.4
Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example, express 36 + 8 as 4 (9 + 2).
Apply and extend previous understandings of numbers to the system of rational numbers.
6.NS.C.5
Understand that positive and negative numbers are used together to describe quantities having opposite directions or values (e.g., temperature above/below zero, elevation above/below sea level, credits/debits, positive/negative electric charge); use positive and negative numbers to represent quantities in real-world contexts, explaining the meaning of 0 in each situation.
6.NS.C.6
Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
6.NS.C.6.A
Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., -(-3) = 3, and that 0 is its own opposite.
6.NS.C.6.B
Understand signs of numbers in ordered pairs as indicating locations in quadrants of the coordinate plane; recognize that when two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
6.NS.C.6.C
Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
6.NS.C.7
Understand ordering and absolute value of rational numbers.
6.NS.C.7.A
Interpret statements of inequality as statements about the relative position of two numbers on a number line diagram. For example, interpret -3 > -7 as a statement that -3 is located to the right of -7 on a number line oriented from left to right.
6.NS.C.7.B
Write, interpret, and explain statements of order for rational numbers in real-world contexts. For example, write -3ºC > -7ºC to express the fact that -3ºC is warmer than -7ºC.
6.NS.C.7.C
Understand the absolute value of a rational numbers as its distance from 0 on the number line; interpret absolute value as magnitude for a positive or negative quantity in a real-world situation. For example, for an account balance of -30 dollars, write |-30| = 30 to describe the size of the debt in dollars.
6.NS.C.7.D
Distinguish comparisons of absolute value from statements about order. For example, recognize that an account balance less than -30 dollars represents a debt greater than 30 dollars.
6.NS.C.8
Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.
Apply and extend previous understandings of operations with fractions.
7.NS.A.1
Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram.
7.NS.A.1.A
Describe situations in which opposite quantities combine to make 0. For example, a hydrogen atom has 0 charge because its two constituents are oppositely charged.
7.NS.A.1.B
Understand p + q as the number located a distance |q| from p, in the positive or negative direction depending on whether q is positive or negative. Show that a number and its opposite have a sum of 0 (are additive inverses). Interpret sums of rational numbers by describing real-world contexts.
7.NS.A.1.C
Understand subtraction of rational numbers as adding the additive inverse, p - q = p + (-q). Show that the distance between two rational numbers on the number line is the absolute value of their difference, and apply this principle in real-world contexts.
7.NS.A.1.D
Apply properties of operations as strategies to add and subtract rational numbers.
7.NS.A.2
Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.
Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (-1)(-1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts.
7.NS.A.2.B
Understand that integers can be divided, provided that the divisor is not zero, and every quotient of integers (with non-zero divisor) is a rational number. If p and q are integers, then -(p/q) = (-p)/q = p/(-q). Interpret quotients of rational numbers by describing real-world contexts.
7.NS.A.2.C
Apply properties of operations as strategies to multiply and divide rational numbers.
7.NS.A.2.D
Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats.
7.NS.A.3
Solve real-world and mathematical problems involving the four operations with rational numbers.
Students will:
Apply and extend previous understandings of multiplication and division to divide fractions by fractions.
6.NS.A.1
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?.
- Background Info. & Guided Practice
- Check for Understanding: Understanding Dividing Fractions by Fractions | Dividing Fractions by Fractions and Whole Number Applications | Dividing Positive Fractions | Dividing Fractions by Fractions Word Problems
- Enrichment Tasks: How Many Containers in One Cup /Cups in One Containers? | Traffic Jam
Compute fluently with multi-digit numbers and find common factors and multiples.
6.NS.B.2
Fluently divide multi-digit numbers using the standard algorithm.
- Background Info.
- Check for Understanding: Multi-Digit Division
- Enrichment Tasks: Interpreting a Division Computation | Setting Goals
6.NS.B.3
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
- Background Info. & Guided Practice
- Check for Understanding: Adding Decimals | Subtracting Decimals | Adding and Subtracting Decimals Word Problems | Multiplying Decimals | Dividing Decimals
- Enrichment Tasks: Jayden's Snacks | Pennies to Heaven
6.NS.B.4
Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example, express 36 + 8 as 4 (9 + 2).
- Check for Understanding: Greatest Common Factor (GCF) | Least Common Multiple (LCM) | GCF and LCM Word Problems | Distributive Property
- Enrichment Tasks: Adding Multiples | Florist Shop
Apply and extend previous understandings of numbers to the system of rational numbers.
6.NS.C.5
Understand that positive and negative numbers are used together to describe quantities having opposite directions or values (e.g., temperature above/below zero, elevation above/below sea level, credits/debits, positive/negative electric charge); use positive and negative numbers to represent quantities in real-world contexts, explaining the meaning of 0 in each situation.
- Check for Understanding: Interpreting Negative Numbers
- Enrichment Tasks: It's Warmer in Miami | Mile High
6.NS.C.6
Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
- Enrichment Tasks: Logical Leaps | Fraction Game
6.NS.C.6.A
Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., -(-3) = 3, and that 0 is its own opposite.
- Check for Understanding: Negative Numbers on the Number Line | Negative Numbers on the Number Line Without Reference to 0 | Number Opposites
- Enrichment Tasks: The Opposite of a Number's Opposite | Zip Zilch Zero
6.NS.C.6.B
Understand signs of numbers in ordered pairs as indicating locations in quadrants of the coordinate plane; recognize that when two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
- Check for Understanding: Graphing Points and Naming Quadrants | Points on the Coordinate Plane | Reflecting Points on the Coordinate Plane
- Enrichment Tasks: Reflecting Points
6.NS.C.6.C
Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
- Check for Understanding: Ordering Negative Numbers | Decimals on the Number Line 3
- Enrichment Tasks: Cake Weighing | Line 'EM Up!
6.NS.C.7
Understand ordering and absolute value of rational numbers.
- Check for Understanding: Finding Absolute Values | Comparing Absolute Values
- Enrichment Tasks: Jumping Flea | Above and Below Sea Level
6.NS.C.7.A
Interpret statements of inequality as statements about the relative position of two numbers on a number line diagram. For example, interpret -3 > -7 as a statement that -3 is located to the right of -7 on a number line oriented from left to right.
- Check for Understanding: Comparing Positive and Negative Numbers on a the Number Line
- Enrichment Tasks: Fractions on the Number Line | Integers on the Number Line
6.NS.C.7.B
Write, interpret, and explain statements of order for rational numbers in real-world contexts. For example, write -3ºC > -7ºC to express the fact that -3ºC is warmer than -7ºC.
- Check for Understanding: Writing Numerical Inequalities
- Enrichment Tasks: Comparing Temperatures
6.NS.C.7.C
Understand the absolute value of a rational numbers as its distance from 0 on the number line; interpret absolute value as magnitude for a positive or negative quantity in a real-world situation. For example, for an account balance of -30 dollars, write |-30| = 30 to describe the size of the debt in dollars.
- Enrichment Tasks: Zip, Zilch, Zero | How Much Did the Temperature Drop?
6.NS.C.7.D
Distinguish comparisons of absolute value from statements about order. For example, recognize that an account balance less than -30 dollars represents a debt greater than 30 dollars.
- Background Info. & Guided Practice
- Check for Understanding: Interpreting Absolute Values
6.NS.C.8
Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.
- Check for Understanding: Coordinate Plane Problems in All 4 Quadrants
- Enrichment Tasks: Distance Between Points
Apply and extend previous understandings of operations with fractions.
7.NS.A.1
Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram.
- Enrichment Tasks: Operations on the number line* | Differences and Distances
- Check for Understanding: Understanding Addition and Subtraction with Negative Numbers | Adding Negative Numbers | Adding and Subtracting Negative Numbers | Adding and Subtracting Negative Numbers Word Problems
7.NS.A.1.A
Describe situations in which opposite quantities combine to make 0. For example, a hydrogen atom has 0 charge because its two constituents are oppositely charged.
- Enrichment Tasks: Bookstore Account | Distances on the Number Line 2*
7.NS.A.1.B
Understand p + q as the number located a distance |q| from p, in the positive or negative direction depending on whether q is positive or negative. Show that a number and its opposite have a sum of 0 (are additive inverses). Interpret sums of rational numbers by describing real-world contexts.
- Background Info. & Guided Practice
- Check for Understanding: Constructing and Interpreting Absolute Value | Understanding Addition and Subtraction with Negative Numbers
7.NS.A.1.C
Understand subtraction of rational numbers as adding the additive inverse, p - q = p + (-q). Show that the distance between two rational numbers on the number line is the absolute value of their difference, and apply this principle in real-world contexts.
- Background Info. & Guided Practice
- Check for Understanding: Subtracting Negative Numbers | Understanding Addition and Subtraction with Negative Numbers
- Enrichment Tasks: Distances Between Houses* | Comparing Freezing Points*
7.NS.A.1.D
Apply properties of operations as strategies to add and subtract rational numbers.
- Background Info. & Guided Practice
- Check for Understanding: Adding and Subtracting Fractions with Unlike Denominators | Adding and Subtracting Negative Fractions, Decimals and Percents
7.NS.A.2
Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.
- Background Info.
- Check for Understanding: Multiplying and Dividing Negative Numbers | Multiplying Positive and Negative Fractions
Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (-1)(-1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts.
- Background Info. & Guided Practice
- Check for Understanding: Multiplying and Dividing Negative Numbers | Multiplying Positive and Negative Fractions
7.NS.A.2.B
Understand that integers can be divided, provided that the divisor is not zero, and every quotient of integers (with non-zero divisor) is a rational number. If p and q are integers, then -(p/q) = (-p)/q = p/(-q). Interpret quotients of rational numbers by describing real-world contexts.
- Background Info. & Guided Practice
- Check for Understanding: Dividing Positive and Negative Fractions
7.NS.A.2.C
Apply properties of operations as strategies to multiply and divide rational numbers.
- Background Info. & Guided Practice
- Check for Understanding: Multiplying Positive and Negative Fractions | Multiplying and Dividing Negative Numbers
7.NS.A.2.D
Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats.
- Background Info.
- Check for Understanding: Converting Fractions to Decimals | Writing Fractions and Repeating Decimals
- Enrichment Tasks: Equivalent fractions approach to non-repeating decimals* | Repeating decimal as approximation*
7.NS.A.3
Solve real-world and mathematical problems involving the four operations with rational numbers.
- Background Info. & Guided Practice
- Check for Understanding: Operations with Rational Numbers
- Enrichment Tasks: Sharing Prize Money* | Anne's Family Trip | School Supplies
|
What are some signs of student mastery?
|
Tools & Technology
These videos show how the number line and counters can support student understanding of: |
More 4 U
View a video on how to divide fractions with tape diagrams. |