Pre-Algebra GT (Grade 6)
2: Geometry (7.G/8.G)
Students understand the statement of the Pythagorean Theorem holds, for example, by decomposing a square in two different ways. They apply the Pythagorean Theorem to find distances between points on the coordinate plane, to find lengths, and to analyze polygons.
Students continue their work with area, solving problems involving the area and circumference of a circle and surface area of three-dimensional objects. In preparation for work on congruence and similarity, they reason about relationships among two-dimensional figures using scale drawings and informal geometric constructions, and they gain familiarity with the relationships between angles formed by intersecting lines. Students work with three-dimensional figures, relating them to two-dimensional figures by examining cross-sections. They solve real-world and mathematical problems involving area, surface area, and volume of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes and right prisms.
Students use ideas about distance and angles, how they behave under translations, rotations, reflections, and dilations, and ideas about congruence and similarity to describe and analyze two-dimensional figures and to solve problems. Students show that the sum of the angle in a triangle is the angle formed by a straight line, and that various configurations of lines give rise to similar triangles because of the angles created when a transversal cuts parallel lines.
Students continue their work with area, solving problems involving the area and circumference of a circle and surface area of three-dimensional objects. In preparation for work on congruence and similarity, they reason about relationships among two-dimensional figures using scale drawings and informal geometric constructions, and they gain familiarity with the relationships between angles formed by intersecting lines. Students work with three-dimensional figures, relating them to two-dimensional figures by examining cross-sections. They solve real-world and mathematical problems involving area, surface area, and volume of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes and right prisms.
Students use ideas about distance and angles, how they behave under translations, rotations, reflections, and dilations, and ideas about congruence and similarity to describe and analyze two-dimensional figures and to solve problems. Students show that the sum of the angle in a triangle is the angle formed by a straight line, and that various configurations of lines give rise to similar triangles because of the angles created when a transversal cuts parallel lines.
What will my child learn?
Students will:
Draw construct, and describe geometrical figures and describe the relationships between them.
7.G.A.2
Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle.
Understand congruence and similarity using physical models, transparencies, or geometry software.
8.G.A.5
Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so.
Understand and apply the Pythagorean Theorem.
8.G.B.6
Explain a proof of the Pythagorean Theorem and its converse.
8.G.B.7
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
8.G.B.8
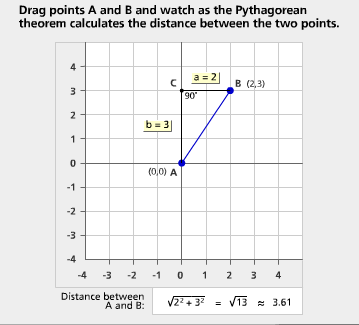
Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.
Understand congruence and similarity using physical models, transparencies, or geometry software.
8.G.A.1
Verify experimentally the properties of rotations, reflections, and translations (see supporting standards that follow):
8.G.A.1.A
Lines are taken to lines, and line segments to line segments of the same length.
8.G.A.1.B
Angles are taken to angles of the same measure.
8.G.A.1.C
Parallel lines are taken to parallel lines.
8.G.A.3
Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
8.G.A.2
Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
8.G.A.4
Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
Draw, construct, and describe geometrical figures and describe the relationships between them.
7.G.A.1
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
Students will:
Draw construct, and describe geometrical figures and describe the relationships between them.
7.G.A.2
Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle.
- Check for Understanding: Triangle Inequality Theorem | Constructing Triangles
- Review/Rewind: Construct a Triangle with Constraints
Understand congruence and similarity using physical models, transparencies, or geometry software.
8.G.A.5
Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so.
- Check for Understanding: Parallel Lines | Equation Practice with Congruent Angles | Finding Angle Measures 1 | Finding Angle Measures 2
- Review/Rewind: Angles, Parallel Lines, and Transversals | Angles in a Triangle Sum to 180 Degrees Proof
- Enrichment Tasks: Find the Missing Angle | Congruence of Alternate Interior Angles via Rotations
Understand and apply the Pythagorean Theorem.
8.G.B.6
Explain a proof of the Pythagorean Theorem and its converse.
- Check for Understanding: Pythagorean Theorem Proofs (Coming Soon)
- Review/Rewind: Bhaskara's Proof of the Pythagorean Theorem,
- Enrichment Tasks: Applying Pythagorean Theorem in a Mathematical Context | Converse of Pythagorean Theorem
8.G.B.7
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
- Check for Understanding: Pythagorean Theorem | Pythagorean Theorem in 3D | Pythagorean Theorem Word Problems | Special Right Triangles
- Review/Rewind: Intro to the Pythagorean Theorem
- Enrichment Tasks: Bird and Dog Race | Running on the Football Field
8.G.B.8
Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.
- Check for Understanding: Distance Formula
- Review/Rewind: Distance Formula
- Enrichment Tasks: Finding Isosceles Triangles | Finding Isosceles Triangles | Finding the Distance Between Points
Understand congruence and similarity using physical models, transparencies, or geometry software.
8.G.A.1
Verify experimentally the properties of rotations, reflections, and translations (see supporting standards that follow):
- Check for Understanding: Perform Reflections
- Review/Rewind: Intro to Geometric Transformations
- Enrichment Tasks: Origami Silver Rectangle
8.G.A.1.A
Lines are taken to lines, and line segments to line segments of the same length.
- Review/Rewind: Rotating Segment About the Origin, Reflecting Line Across Another Line
8.G.A.1.B
Angles are taken to angles of the same measure.
8.G.A.1.C
Parallel lines are taken to parallel lines.
- Check for Understanding: Properties of Rigid Transformations
8.G.A.3
Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- Check for Understanding: Perform Translations
- Review/Rewind: Translations of Polygons | Rotations of Polygons | Reflections and Mapping Points | Dilating Shapes: Shrinking
- Enrichment Tasks: Triangle Congruence with Coordinates | Reflecting Reflections
8.G.A.2
Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
- Check for Understanding: Exploring Rigid Transformations and Congruence
- Review/Rewind: Congruent Shapes and Transformations | Performing Sequences of Transformations
- Enrichment Tasks: Congruent Rectangles | Congruent Segments
8.G.A.4
Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
- Check for Understanding: Exploring Angle-Preserving Transformations and Similarity
- Review/Rewind: Similar Shapes & Transformations
Draw, construct, and describe geometrical figures and describe the relationships between them.
7.G.A.1
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
- Check for Understanding: Constructing Scale Drawings | Interpreting Scale Drawings
- Review/Rewind: Solving a Scale Drawing Word Problem | Making a Scale Drawing
- Enrichment Tasks: Floor Plan | Map Distance
|
What are some signs of student mastery?
|
Tools & Technology
GeoGebra is a dynamic math software tool that allows users to explore geometry, algebra, tables, graphing, statistics and other areas of math in one easy-to-use package. It can be downloaded for FREE on a computer or tablet device. Angle Sums (NCTM) Example the sums of angles in various polygons. Discover the relationship between the sides and the sum of their angles. Exploring square roots (Learn Alberta) Use the squares to apply the Pythagorean Theorem. Transmographer (Shodor) Practice translating, reflecting, and rotating on a coordinate plane. Algebraic Transformations (NCTM) Explore the effects of various transformations. |
More 4 U
Looking for more info. on Applications of the Pythagorean Theorem? Here's a resource that helps students use the power of algebra to solve geometry problems (8.G.B.8). Source: Annenberg Learner, 2014
|